«Hvor mye tåler du at pengene dine svinger i verdi?»
Det er spørsmål som ofte går igjen i bankenes fondsveiledere, eller når rådgivere skal gi kundene tilpassede investeringsstrategier.
Problemet er at vi er dårlige på å forutse følelser og reaksjoner på fremtidige hendelser.
Vi klarer selvfølgelig å treffe på hva som vil gjøre oss glade eller sinte (vinne i lotto / frastjålet sykkel). Men det er intensiteten og varigheten vi har en tendens til å over- og undervurdere (Wilson & Gilbert, 2003).
Uten erfaring fra lignende hendelser, vil svaret du oppgir mer eller mindre basere seg på gjetting. Kanskje nyttig som ansvarsfraskrivelse. Ikke særlig nyttig for å kartlegge risikoprofilen din.
Her er faktorer som mål, tid og likviditet, langt mer nyttig når det kommer til å lage en fornuftig investeringsplan med komfortabel risiko.
Men først: det mest brukte risikomålet.
Ta en titt på disse tre grafene:
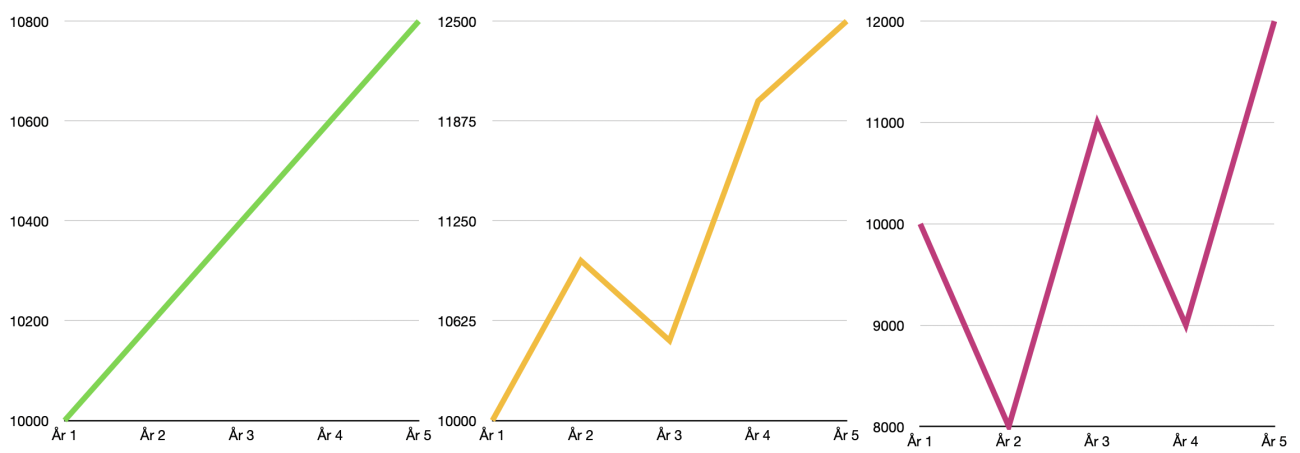
Hvilken graf assosierer du med høyest risiko?
…
Den siste, ikke sant?
Større svingninger betyr høyere risiko. Det er intuitivt.
Kvantifisere risiko
Det er flere ulike metoder og mål på å tallfeste risiko.
Standardavvik er av de mest kjente og et godt utgangspunkt. I tillegg er det flere modeller som bygger videre på dette risikomålet.
Det er også det denne risikoskalaen, som du helt sikkert har sett tidligere, baserer seg på:

Denne blir kalt for «synthetic risk and reward indicator», og brukes som felles måleenhet for europeiske fond. Hensikten er gjøre det enklere for investorer å forstå risikoprofilen og sammenligne med andre fond.
Tallene deles opp etter hvor høyt standardavviket er:
- 1 = < 0,5 %
- 2 = 0,5-2 %
- 3 = 2-5 %
- 4 = 5-10 %
- 5 = 10-15 %
- 6 = 15-25 %
- 7 = > 25%
Det forteller oss hvor langt unna avkastningen har beveget seg fra gjennomsnittet – jo større bevegelser fra gjennomsnittet, desto høyere risiko.
For å beregne standardavviket trenger vi kun:
- Gjennomsnittlig avkastning
- Variasjonen fra gjennomsnittet
Last ned malen vår på beregning av standardavvik i Excel
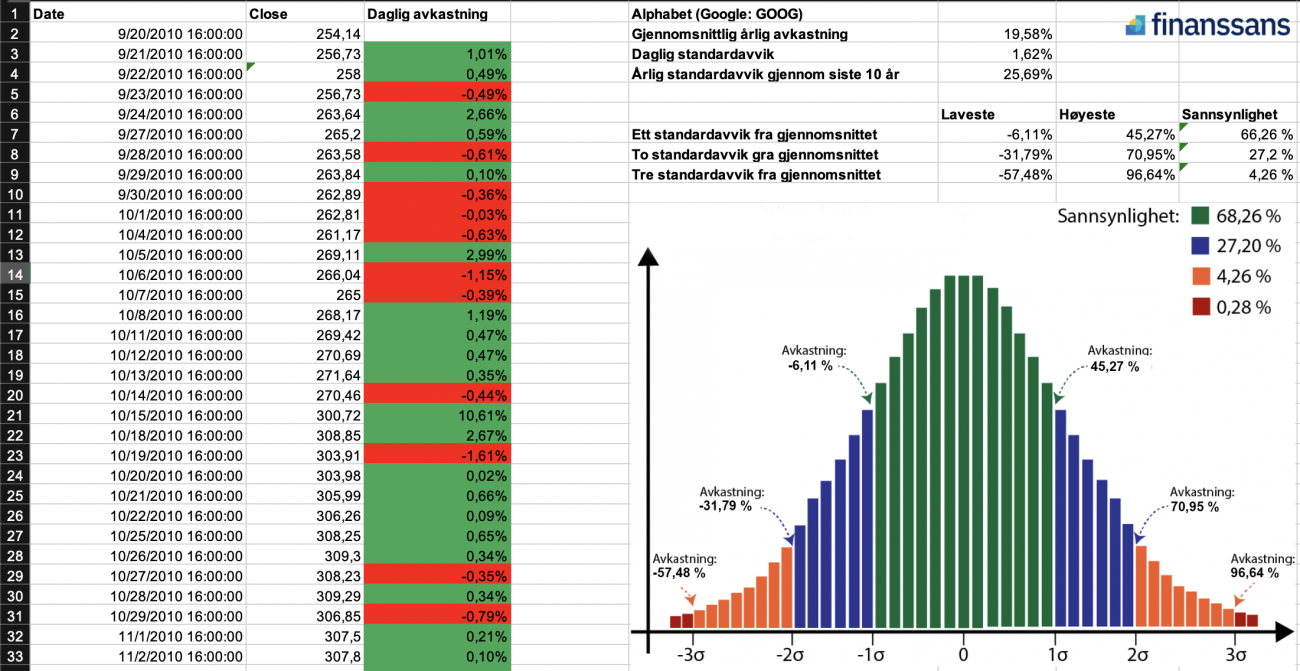
I vårt eksempel regnet vi ut at Alphabet (Google – ticker: «GOOG») gjennomsnittlig årlig avkastning fra de siste 10 årene, er 19,58 %.Under samme periode har årlig standardavvik vært 25,69 %.Og det forteller deg kanskje ikke så mye.Det er først når vi ser det i en normalfordeling at risikoen kommer tydeligere frem:
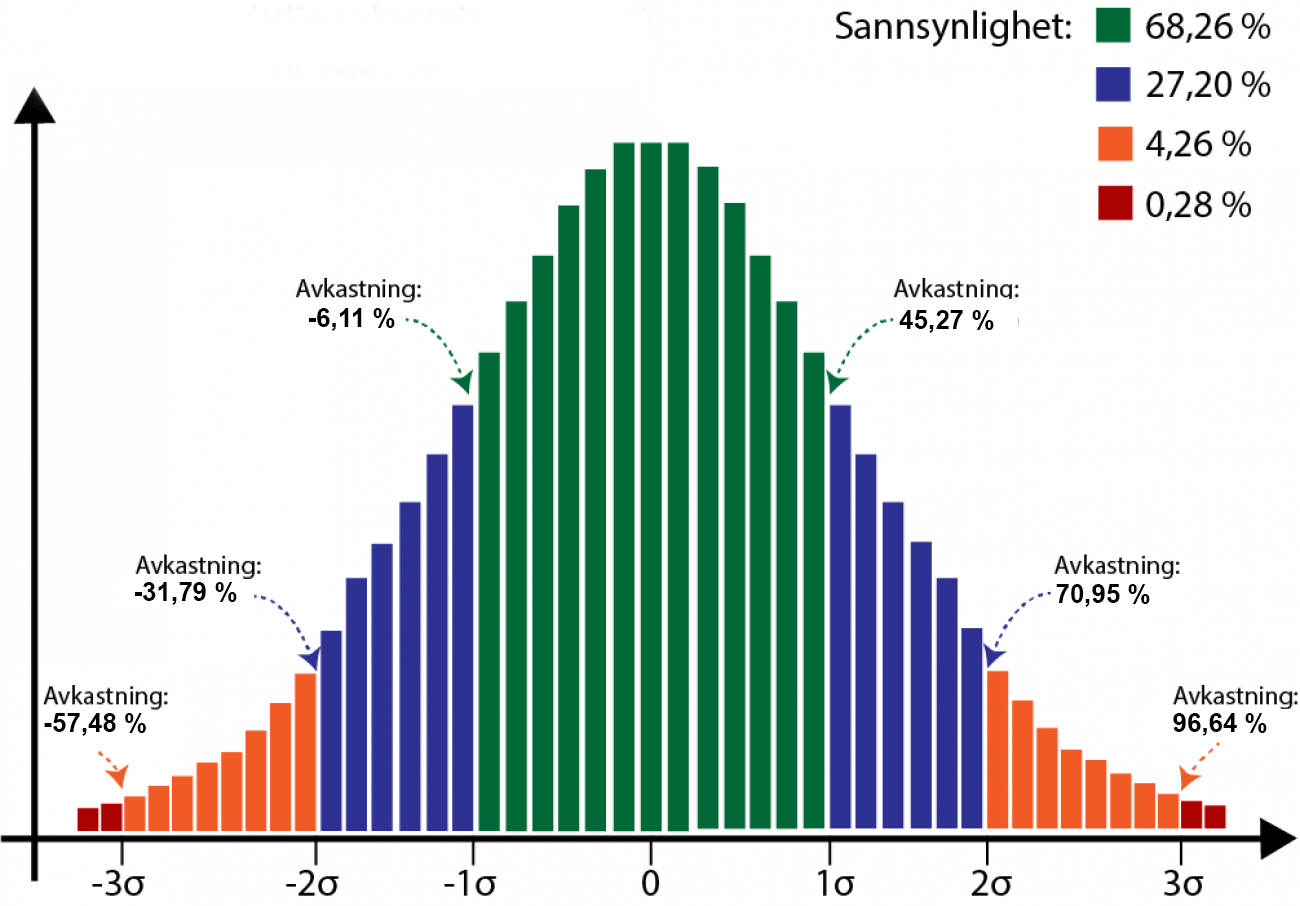
I normalfordeling (empirisk regel) fordeles sannsynligheten alltid som følgende:
- 68,26 % av tilfellene faller inn mellom -1 og 1 standardavvik over gjennomsnittet
- 27,2 % mellom -2 og -1 og mellom 1-2
- 4,26 % mellom -3-2 og mellom 2-3
- Dermed er 99,72 % av tilfellene forventet å havne et sted mellom tre standardavvik under gjennomsnittet og tre standardavvik over gjennomsnittet.
Med «Alphabet-aksjens» gjennomsnittlig avkastning på 19,58 % og standardavvik på 25,69 %, blir fordelingen slik:
- Ett standardavvik under gjennomsnittet = -6,11 % (19,58-25,69)
- Ett standardavvik over gjennomsnittet = 45,27 % (19,58+25,69)
- To standardavvik under gjennomsnittet = -31,79 % (19,58-25,69-25,69)
- To standardavvik over gjennomsnittet = 70,95 % (19,58+25,69+25,69)
- …
Det er altså 68,26 % sannsynlighet for at den årlige avkastningen til Google blir mellom -6,11 % og 45,27 %.
Strekker vi oss én utover i fordelingen, er det 95,46 % (68,26+27,2) sannsynlighet for at avkastningen havner et sted mellom -31,79 % og 70,95 %.
Er aksjemarkedet normalfordelt?
Med utgangspunkt i sannsynlighetene ovenfor, vil Alphabet-aksjen overstige 50 % årlig avkastning omtrent hver 8 og et halvt år (se beregning nedenfor).
Det høres ikke helt feil ut, når vi ser at det har vært tilfelle i ett av de siste 10 årene (58 % i 2013), og nesten-tilfelle i 2015 (47 %).
For S&P 500-indeksen har gjennomsnittlig årlig avkastning vært cirka 8 % og standardavvik på cirka 14 % de siste 30 årene.
Sannsynligheten for at avkastningen overstiger 25 %, er 11,2 %. Det tilsier at det skal gå omtrent 9 år mellom hver gang, eller 3,3 ganger på 30 år. I realiteten har indeksen klart det 7 ganger i løpet av denne perioden.
P (X > 0,5) = P (Z > 0,5-0,1958) / 0,2569 = P (Z > 1,1849) = 1- 0,8820 (bruk z-tabell) = 1 / 0,118 = 8,47 ≈ 8,5 år.
Hva forteller det oss?
At normalfordeling ikke er et perfekt mål på risiko i aksjemarkedet.
Ekstremverdier oppstår oftere enn hva sannsynlighetene forteller oss. Dette er kjent som »fat tail risk», hvor venstresiden av fordelingen er det som bekymrer oss. I tillegg ser vi i perioder og i ulike aktiva, asymmetri i fordelingen.
Standardavvik gir oss derimot et raskt overblikk på volatiliteten. Vi kan bruke den til å se investeringens tidligere svingninger – og dermed risiko – og velge etter ønsket risikoprofil. Den er også nyttig når vi setter sammen porteføljer, og til å sammenligne lignende aksjer og fond med hverandre. (Husk å bruk samme tidsperiode når du sammenligner standardavvik. Risikoskalaen ovenfor ser 5 år tilbake).
Markedsrisiko og selskapsrisiko
Når vi investerer i aksjer eller andre verdipapirer, utsettes vi for to typer risiko:
- Markedsrisiko (systematisk risiko)
- Selskapsrisiko (usystematisk risiko)
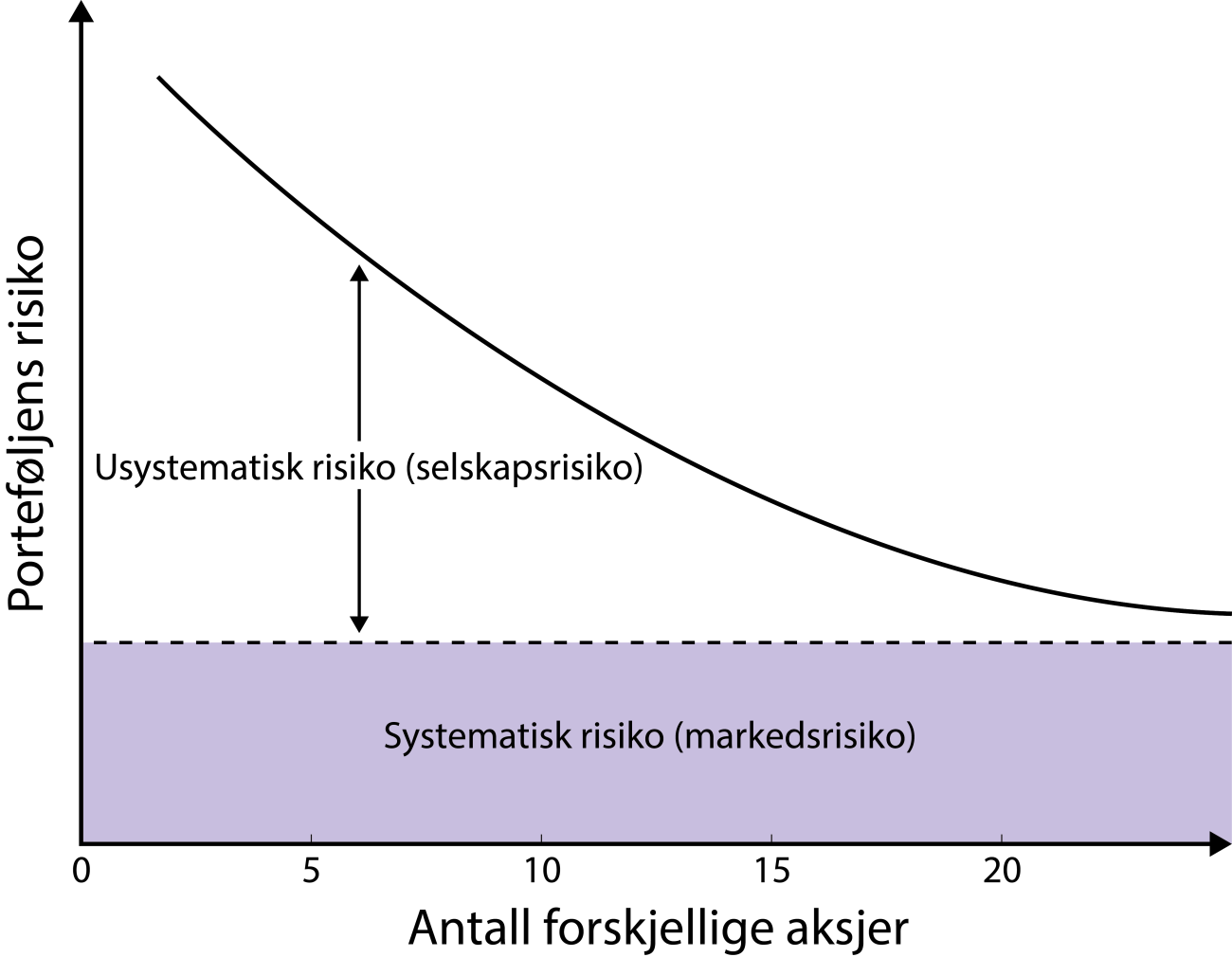
Markedsrisikoen påvirker hele markedet. Det kan for eksempel være risikoen for naturkatastrofer, inflasjon, renter, atferdsendringer eller … Covid-19.
Vi får altså ikke redusert denne risikoen ved å eie aksjer i flere selskaper.
Selskapsrisikoen gjelder spesifikt for selskapet eller bransjen. Det kan blant annet være risikoen for at forretningsmodellen mislykkes, eller at det innføres politiske vedtak som påvirker bransjen.
Denne risikoen kan vi redusere med diversifisering, som illustreres i grafen ovenfor.
Diversifisering – den eneste gratis lunsjen du får
Du har helt sikkert hørt det før:
«Ikke legg alle eggene i samme kurv».
Det er åpenbart for å redusere risikoen. Men det som ikke er like opplagt, er at vi kan få det til uten å redusere forventet avkastning. Gratis lunsj!
Slik fungerer det:
Selskap A selger iskrem. Aksjen gjør det bra når det er sol, men dårlig når det regner.
Selskap B selger paraplyer. Aksjen gjør det bra når det regner, men dårlig når det er sol.
Begge selskapene har en forventet avkastning på 10 prosent. Aksjene beveger seg ulikt – de har en negativ korrelasjon med hverandre.
Ved å investere likt i begge selskapene, oppnår vi samme forventede avkastning på 10 prosent, men siden aksjenes svingninger utjevner hverandre til en viss grad, vil porteføljen svinge mindre i verdi (som betyr lavere risiko).
Hvor mange aksjer er det nødvendig å ha i porteføljen?
I en studie av Elton og Gruber (1977) ble samtlige aksjer notert på «New York Stock Exchange» (NYSE) gjennomgått, for å gi et svar på hvor mye selskapsrisikoen reduseres etter x-antall tilfeldige aksjer i porteføljen.
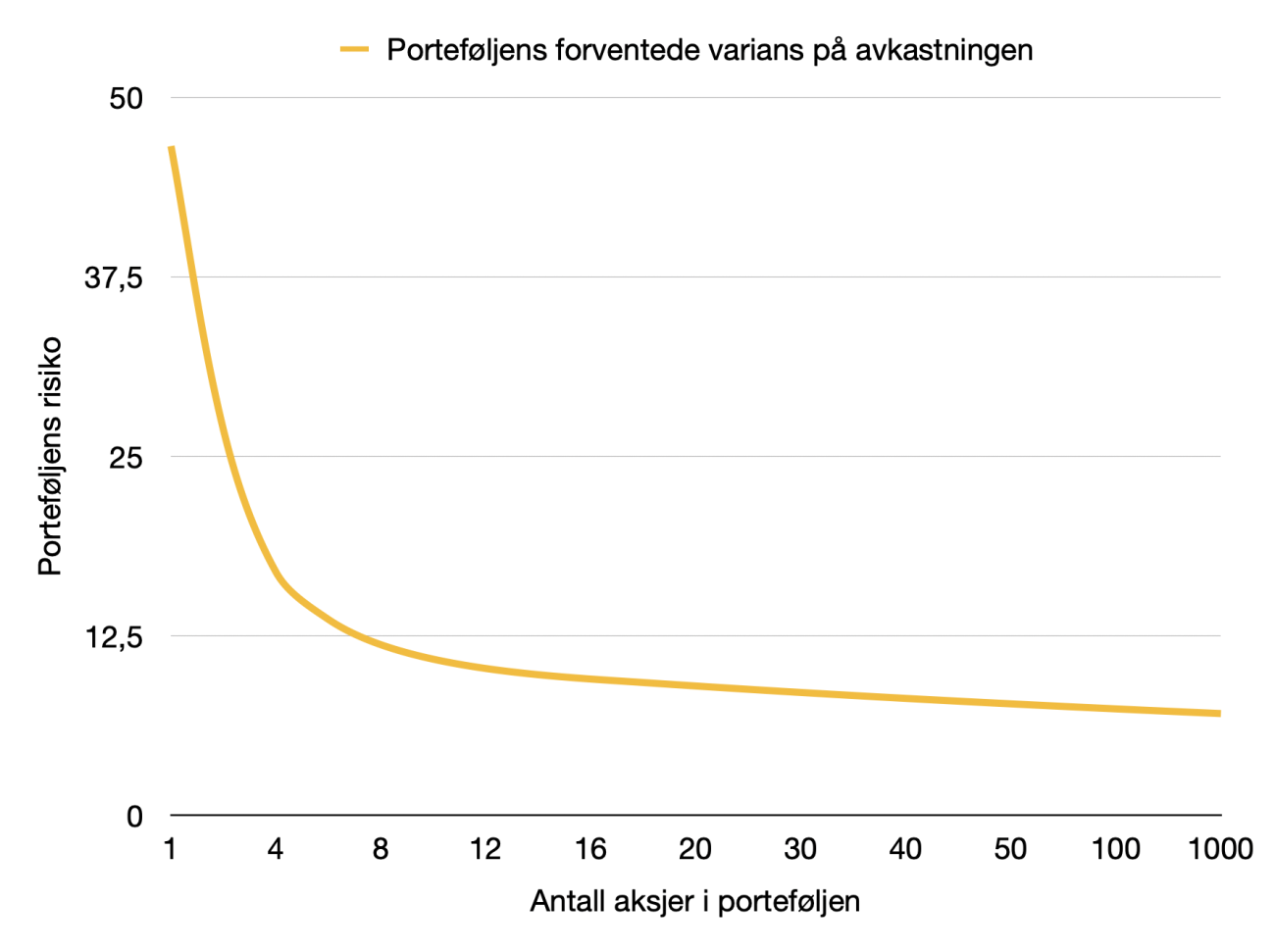
Resultatet viser at diversifiseringseffekten er størst til å begynne med. Ved å gå fra én til to forskjellige aksjer i porteføljen, reduserte risikoen med hele 42 % (fra 46,6 til 26,8 i forventet varians).
Den marginale effekten avtar etter hvert som flere aksjer legges til i porteføljen. Det er derfor lite hensiktsmessig å legge til mer enn 30 ulike aksjer, om hensikten kun er å oppnå lavest mulig (usystematisk)risiko. Da kunne vi med fordel heller investert i et globalt indeksfond.
Risikojustert avkastning
Fond A sin avkastning er 15 %. Fond B sin avkastning er 8 %.
Hvilket fond er best?
Svaret er selvfølgelig Fond A, om vi kun ser på avkastningen. Men hva om halvparten av porteføljen i Fond B består av obligasjoner med lav risiko, i motsetning til Fond A som kun består av aksjer.
Er Fond A fortsatt best?
Det er dette risikojustert avkastning skal gi deg svaret på.
Det er flere metoder å måle dette på, men det vanligste er å bruke Sharpe Ratio. Og det forklares kanskje enklest ved å gå gjennom formelen:
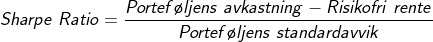
Porteføljens avkastning fratrukket risikofri rente (for eksempel 10-årig norsk statsobligasjon), er det som kalles for risikopremie – «premien» vi forventet å oppnå ved å ta risiko.
Dette divideres med porteføljens standardavvik. Slik at høyere risiko på samme risikopremie, gir lavere Sharpe Ratio. Jo høyere Sharpe Ratio, desto bedre er det.
Optimalisere porteføljen med Sharpe ratio
La oss si at du setter opp en aksjeportefølje bestående av ti ulike selskaper. Du skal investere 100.000 kroner totalt.
Hvordan skal du fordele pengene?
10 prosent i hvert selskap?
Fordele pengene etter selskapenes markedsverdi? (hvis Equinor utgjør 50 % av porteføljens markedsverdi, skal tilsvarende andel investeres i selskapet).
Eller du kan la Sharpe Ratio avgjøre. Altså velge vektfordeling som gir høyest risikojustert avkastning.
(Til info er nok Sharpe ratio mer nyttig til å måle porteføljens/fondets resultater, enn å forutse fremtidige resultater.)
Slik gjør du det:
Det enkleste metoden er å bruke Excel:
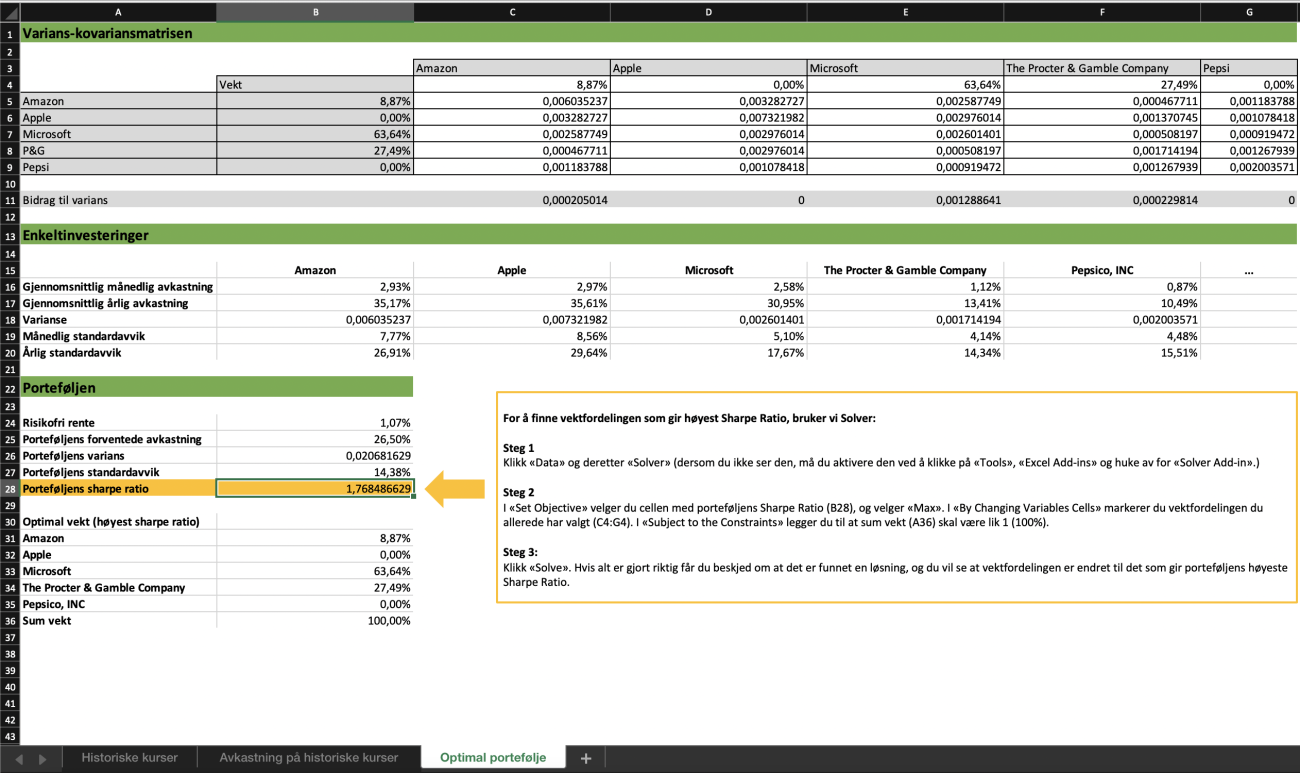
Beregning av Sharpe ratio i Excel
Last ned historisk data på det du vil ha i porteføljen. Vi henter data fra Yahoo Finance, med 5 års historikk og månedlig intervall i dette tilfellet.
Beregn avkastningen. Bruk =LN(nåværende måned/forrige måned).
Sett opp Varians-kovariansmatrise (nødvendig for mer enn to variabler). Bruk =var.s når det er samme selskap, og =covariance.s på ulike selskaper.
Beregn porteføljens standardavvik og avkastning. Legg også til risikofri rente.
Beregn Sharpe Ratio med vektfordeling før optimalisering. Bruk «Solver» får å maksimere Sharpe Ratio ved å endre fordelingen.
En mer detaljert forklaring ser du i Excel-malen.
Nedsiderisiko
Svingninger brukes som mål på risiko: «Investeringer i aksjemarkedet krever at du tåler store verdisvingninger».
Men om investeringen skulle det gjøre det bedre enn forventet, regner du det som økt risiko?
For det som egentlig bekymrer oss er nedsiden. Hva stor er sannsynligheten for negativ avkastning, eller at investeringen gjør det dårligere enn forventet?
Når positive overraskelser regnes som premie, og ikke risiko, må vi utelukke svingninger som skjer over et visst punkt. Ofte settes grensen på 0 %, men det kan i utgangspunktet være hver enkeltes individuelle grense. Dette er illustrert som «forventet avkastning» i diagrammet nedenfor.
Mer rettferdig sammenligning av prestasjoner med Sortino-raten
La oss si du skal sammenligne to aktivt forvaltede fond innenfor samme sektor, A og B. Begge har som mål å oppnå høyest mulig avkastning.
| Fond A | Fond B |
|---|---|
| 100 | 100 |
| 210 | 80 |
| 120 | 100 |
| 160 | 60 |
| 120 | 119 |
| 20 % avkastning | 19 % avkastning |
Basert på tidligere avkastning, er fond A best.
Derimot har verdien på fond A beveget seg mer fra gjennomsnittet enn fond b, slik at standardavviket er høyere.
| Fond A | Fond B | |
|---|---|---|
| Standardavvik | 68,92 % | 61,35 % |
For å få med i beregningene at fond A har tatt større risiko, bruker vi Sharpe-raten for å finne risikojustert avkastning:
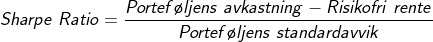
Forutsatt 1,3 % risikofri rente, blir dette resultatet:
Here’s the Markdown code for the table with the Sharpe Ratio row:
| Fond A | Fond B | |
|---|---|---|
| Sharpe-raten | 0,27 | 0,28 |
Basert på risikojustert avkastning ved sharpe-raten, er fond B best.
Men legg merke til at dersom du investerte i fond A, ville du aldri opplevd at verdien falt lavere enn innskuddet. Derimot har fond B vært på nedsiden i to perioder, hvor den ene tilsvarte et urealisert tap på 40 % av innskuddet.@
Sharpe-raten, som tar høyde for svingninger oppover og nedover, gir det derimot inntrykk av at fond B er det tryggeste alternativet.
Ville du heller foretrukket at verdien på fondsandelene dine gikk fra 100 til 150, og ned til 100 igjen, eller fra 100 til 50, og tilbake til 100?
Løsningen er Sortino-raten
Både Sortino- og Sharpe-raten, bruker standardavvik som risikomål.
Forskjellen er at Sortino-raten kun ser på bevegelser som skjer under minimumskravet, for eksempel 0 %. Den «straffer» ikke positiv volatilitet. Den gir oss et mål på hvor mye meravkastning vi får pr. del av nedsiderisikoen. Så jo høyere tall, desto bedre er det.
Det gir også mening når vi vet at frustrasjonen av å tape 1 000 kroner, overstiger gleden av å vinne 1 000 kroner – det er asymmetri i tap vs. gevinst (prospektteori).
Formelen ser slik ut:

For å finne standardavviket til nedsiden, legger vi kun til periodene med mindreavkastning. Det kan for eksempel være alle negative avkastninger, eller som er lavere enn minimumskravet, også kjent som MAR («Minimum Acceptable Return»).
Eksempel:
-2 % avkastning betyr mindreavkastning på -2 % hvis grensen er satt til 0 %, eller -3 % hvis grensen er satt til 5 % (5-2).
Her er grensen satt til 0 %.
| Periode | Mindreavkastning - Fond A | Mindreavkastning - Fond B |
|---|---|---|
| Periode 1 | 0 % | -20 % |
| Periode 2 | -42,86 % | 0 % |
| Periode 3 | 0 % | -40 % |
| Periode 4 | -25 % | 0 % |
Ved å kun måle svingninger på nedsiden, blir standardavviket ulikt enn det vi så ovenfor.
| Fond A | Fond B | |
|---|---|---|
| Nedsidens standardavvik | 12,63 % | 14,14 % |
| Sortino-raten | 1,58 | 1,34 |
Fond B har hatt større svingninger på nedsiden, slik at basert på risikojustert avkastning ved Sortino-raten, er fond A best.
Oppsummert var fond A beste valg basert på tidligere avkastning, fond B best på risikojustert avkastning målt ved Sharpe-raten, og fond A best på risikojustert avkastning mål ved Sortino-raten.
Uavhengig av hvilke nøkkeltall man foretrekker, er det viktig å huske på at samtlige er basert på historikk, og at det kan være helt andre resultater i fremtiden.
Last ned Sortino rate-malen vi har laget i Excel. Den sammenligner Sortino-raten for de populære børsfondene (ETF) ARK Innovation og Vanguard Information Technology.

