Netto nåverdi (nåverdimetoden)

Nåverdimetoden er en enkel og hensiktsmessig metode for å vurdere investeringer.

Det blir brukt som lønnsomhetsanalyse til å se om en investering er lønnsom eller ikke – vi diskonterer fremtidige kontantstrømmer til dagens verdi.

Denne artikkelen inneholder enkle forklaringer og eksempler på beregninger av nåverdi. Det inkluderer også nedlastbar fil i Excel, samt fremgangsmåten på Texas Instruments BA II Plus-kalkulator.

Nåverdimetoden er en lønnsomhetsanalyse som brukes til å se om en investering er lønnsom eller ikke. Det blir gjort ved å diskontere fremtidige kontantstrømmer til dagens verdi.

Formel og regel

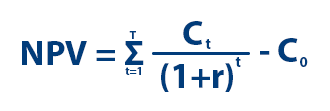
• NPV = Netto nåverdi (Net Present Value)
• Ct = Innbetalingsoverskuddet i år t
• r = Diskonteringsrenten (avkastningskravet)
• t = Levetiden
• C0 = Investeringsutgiften

Ved ubegrenset tilgang på kapital er regelen:

Netto nåverdi ≥ 0 (lønnsom) Netto nåverdi < 0 (ulønnsom)

Hvis tilgangen på kapital er begrenset velges investeringen med høyest netto nåverdi.

Diskonteringsrenten

Diskonteringsrenten er avkastningskravet justert for risiko.

Avkastningskravet er den laveste avkastningen en aksepterer for at investeringen skal bli lønnsom. For å fastsette avkastningskravet kan man se på lignende investeringer som man har tilgang til og dens forventede avkastning. Renten kan også fastsettes etter kapitalverdimodellen.

Basert på estimater

Nåverdimetoden forutsetter at vi kjenner til investeringsutgiften, kontantstrømmen, levetiden og avkastningskravet. Men hvor ofte har du ikke hørt om et prosjekt som overskrider budsjettet? Eller at prosjektet har tatt lenger tid enn planlagt? Det samme gjelder for forventede innbetalinger; det kan bli lavere enn først antatt.

I tillegg kan renten endres underveis i prosjektets levetid, eller at oppstår andre hendelser som påvirker avkastningskravet. Det gjør at netto nåverdi på investeringen blir betydelig ulik fra beregningene.

Mye av usikkerheten kan «løses» ved å gjenspeile det i avkastningskravet. Det kan også være en fordel å sette opp ulike scenarioer med tilhørende sannsynlighet, for eksempel lav (20 %), middels (60 % og høy (20 %), for så å beregne forventet netto nåverdi.

Eksempel på beregning av netto nåverdi

Du vurderer å investerer 100.000 kroner i et prosjekt, med en levetid på tre år. Det er forventes at prosjektet utbetaler 50.000, 60.000, 70.000 kroner for henholdsvis år 1,2 og 3. Avkastningskravet er beregnet til 10 prosent. Er investeringen lønnsom?

Kontantstrømoppstilling

For å få oversikt er det lurt å sette inn ut- og innbetalingene inn i en kontantstrømoppstilling:

Here is the markdown version of the data:

	Nå	År 1	År 2	År 3
Investeringsutgift	-100.000	0	0	0
Utbytte	0	50.000	60.000	70.000

Netto nåverdi

Investeringen er lønnsom siden nåverdien er større eller lik 0.

Fremgangsmåte for Excel:

Klikk her for å laste ned mal på netto nåverdi beregning (inkludert XNPV) i Excel.

Fremgangsmåte for Texas Instruments BA II Plus:

• Slett eventuelt eksisterende tall: CF - 2ND - CE|C
• Legg inn investeringsutgiften i CFo: CF - 100000 - +|- - ENTER
• Legg inn resten av kontantstrømmene: - 50000 - ENTER - - - 60000 - ENTER - - - 70000 - ENTER
• Legg inn avkastningskravet: NPV - 10 - ENTER
• Beregne netto nåverdi: - CPT = 47.633,35

Tidens innvirkning på nåverdien

De fleste investeringer innebærer en kostnad i begynnelsen, for så å motta en eller flere innbetalinger på et senere tidspunkt. Tidspunktet på når innbetalinger oppstår påvirker nåverdien. Vi deler tidens kostnader inn i følgende:

• Tidskostnad – Vi foretrekker 100 kroner i dag enn 100 kroner om et år. Vi må kompenseres for utsatt forbruk og glipp av andre muligheter til å investere pengene på.
• Inflasjonskostnad – 100 kroner i dag er mer verdt enn om et år. For at pengenes kjøpekraft skal opprettholdes må avkastningen være minst like høy som prisstigningen.
• Usikkerhetskostnad – 100 kroner utbetalt nå er sikrere enn 100 kroner utbetalt om fem år. Man risikerer at pengene aldri blir utbetalt, eller at man får utbetalt et annet beløp enn planlagt.

Eksempel:

Avkastningskrav = 10 %	Case A	Case B
Nå	-100.000	-100.000
År 1	50.000	10.000
År 2	40.000	20.000
År 3	30.000	30.000
År 4	20.000	40.000
År 5	10.000	50.000
Netto nåverdi	20.921	16.526

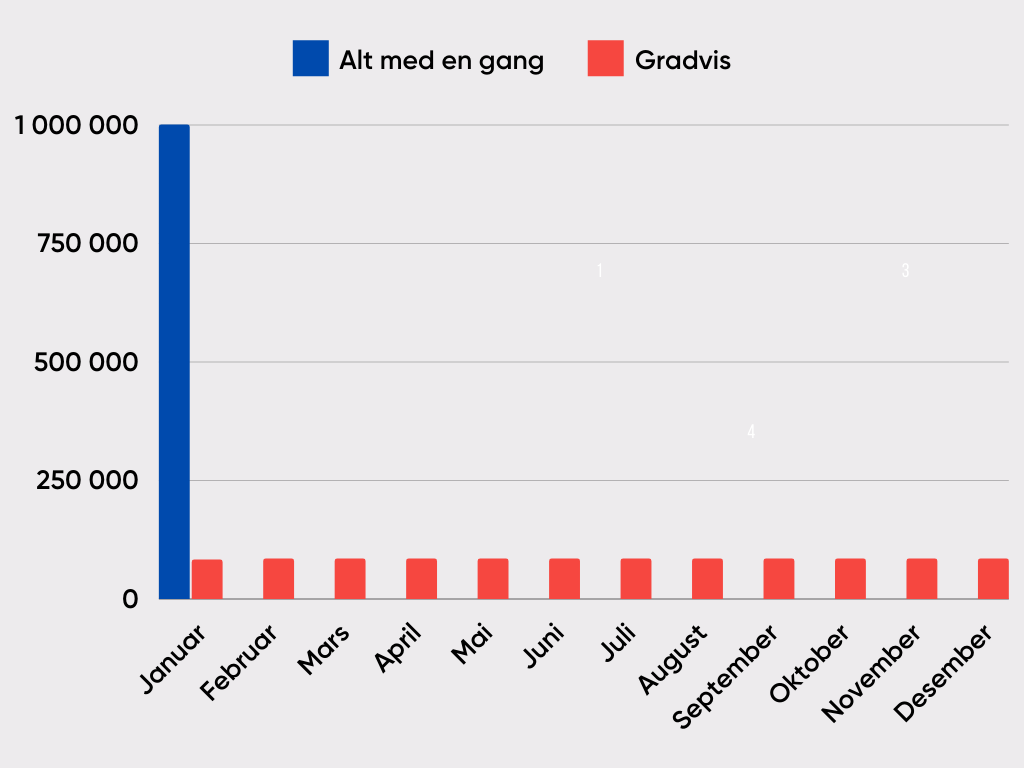
Selv om det blir utbetalt like mye i Case A og B, har førstnevnte en høyere nåverdi siden de høyeste utbetalingene skjer tidligere i prosjektets levetid.

Spørsmål og svar

Hva er forskjellen på netto nåverdi og nåverdi?

Nåverdi er kontantstrømmene i dagens verdi. Netto nåverdi er også kontantstrømmene i dagens verdi, men fratrukket investeringsutgiften (C0).

Hva om ikke utbetalingene skjer på slutten av hvert år?

For enkelthetens skyld tar formelen utgangspunkt i at alle utbetalingene skjer i slutten av hvert år eller hver periode. I praksis vil det åpenbart ikke være slik.

Hvis utbetalingene skjer jevnt utover hele året:

Opphøyelsen i det andre året byttes ut fra 1 til 1,5, fra det tredje året fra 2 til 2,5 og så videre.

Hvis utbetalingene skjer på uregelmessige intervaller:

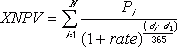
• di = Den ente, eller siste utbetalingsdato
• d1 = Første utbetalingsdato
• Pi = Den ente, eller siste utbetalingssum

Eksempel:

=-500/((1+0.1)^((“1/1/2017”-“1/1/2017”)/365)) + 1000/((1+0.1)^((“2/1/2018”-“1/1/2017”)/365))